Many people have tried to answer this question in several different ways – some dealing with physics of sound and the overtone series, others with the history of keyboard instruments and tuning theory and even some dealing with the resonance of the universe whatever that means… What I plan to do is not to give you a short but complete answer to the question, but rather outline some of the flaws in certain kinds of reasoning and stress the importance of taking a holistic approach involving many theories.
Although still to this day not entirely understood, human hearing is thought to be two fold meaning that we have the ability to process two types of input – musical and sonic. An example of sonic hearing would be the ability to distinguish two peoples voices when they sing the same note. Musical hearing would be more so the ability to distinguish two different notes sang by the same person as being different in pitch. We will focus on musical hearing.
Humans can hear between 20 and 20000Hz. Globally all cultures identify an equivalence class within this range called an octave. That is people consider two frequencies musically the same (i.e the same tone or note) if one is twice the other. So 55Hz and 110Hz are both the same note which we happen to call A. So lets zoom into our frequency spectrum and consider one octave from A2=110Hz to A3=220Hz.
Although all cultures agree on the octave as an equivalence relation, different cultures divide the octave differently. Here is a table from researchgate that shows some diversity among cultures. 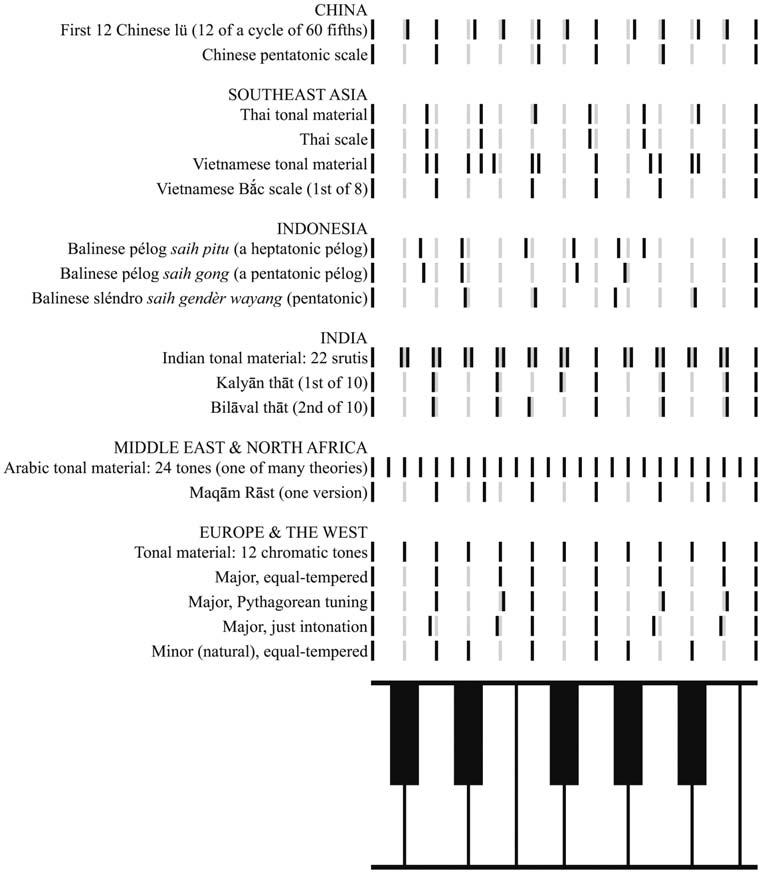
The fact that so many of these divisions are either 5 notes or 7 notes is in itself interesting and is perhaps the root of the question why 7 white and 5 black notes. Maybe a similar analogy could be made with colors. English speakers identify about 12 colors
- red
- orange
- yellow
- green
- turquoise/teal/indigo
- blue
- purple
- pink
- white
- grey
- brown
- black
while when talking about the spectrum of colors – the colors of the rainbow – identify 7
- red
- orange
- yellow
- green
- blue
- indigo
- purple
It is very hard to understand why we draw lines where we do. I would say nearly impossible without been biased towards physics – acoustics and the overtone series, mathematics – small integer ratios and the resonance of the universe or history – development of instruments and nationalistic tuning standards. That being said, if you can accept the fact that for all of history man has been singing 7 note scales then understanding the layout of the piano keyboard is much easier.
Since the keyboard is a Western instrument we will focus only on divisions of the octave from Europe and The West.
Just intonation is without a doubt the most natural sounding of the Western tuning system. That is, if a westerner were to sing a major scale they would naturally sing in just intonation. If you can accept this fact alone the explanation for the 7 white notes and 5 black is very easy:
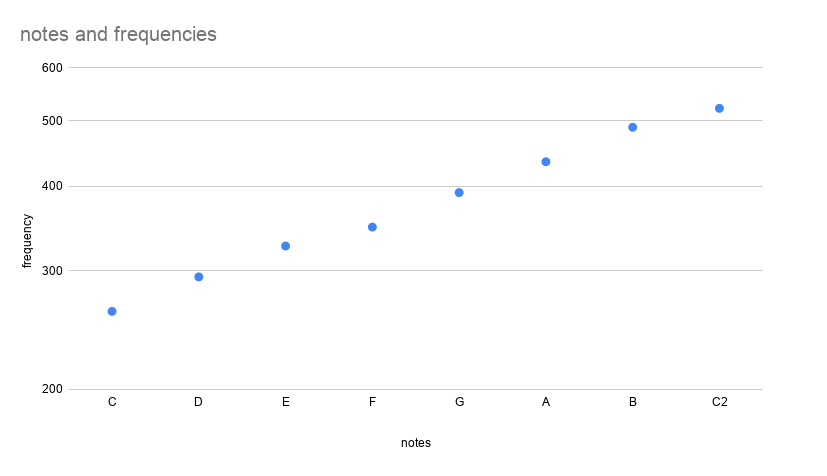
The Just Intonation scale uses the following ratios:
C=1
D=9/8
E=5/4
F=4/3
G=3/2
A=5/3
B=15/8
C2=2 (C one octave higher)
Here is a just intonation scale on a number line from 1 to 2:

As you can see on the line, the distance from C to D is the same of that from B to C2. they are both 1/8 away 9/8 – 1 = 2 – 15/8 = 1/8. Peoples musical hearing would however argue that these two intervals are significantly different and tend to call C to D a whole tone and B to C2 a semitone. This is why it is important to view frequencies using a logarithmic scale. Here are the same notes on a logarithmic scale
here is a keyboard layout to play that scale:
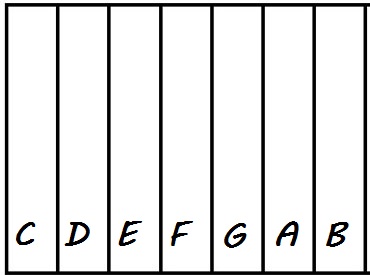
As you can see
and here is the hydraulis – one of the oldest keyboard instruments with this layout. It was actually tuned to the Greater Perfect System which would have been very close to just intonation since the fourth was perfect – a 4:3 ratio.