Still to this day we don’t understand exactly why certain sounds are more pleasing then others. What happens beyond the physical level is still not entirely understood. This investigation aims to gain an insight as to how our minds process auditory information and why some sounds sound better than others.

I will first explore Galileo’s coincidence (or pulse) theory of consonance. He claimed consonances are pairs of tones that strike the ear drum with regularity. He proposed that the sensation of consonance is a result of the ear drum beating less often.  If two frequencies have a simple integer ratio (say 3:2) then they will align often and thus your ear drum will beat one less time for each time they align. Think about each dot as your ear drum beating for each frequencies 1 2 and 3. Frequencies 1 and 3 are consonant because they often align and frequency 2 is dissonant with frequency 1 (and also with frequency 3) because they never align (well not in this drawing).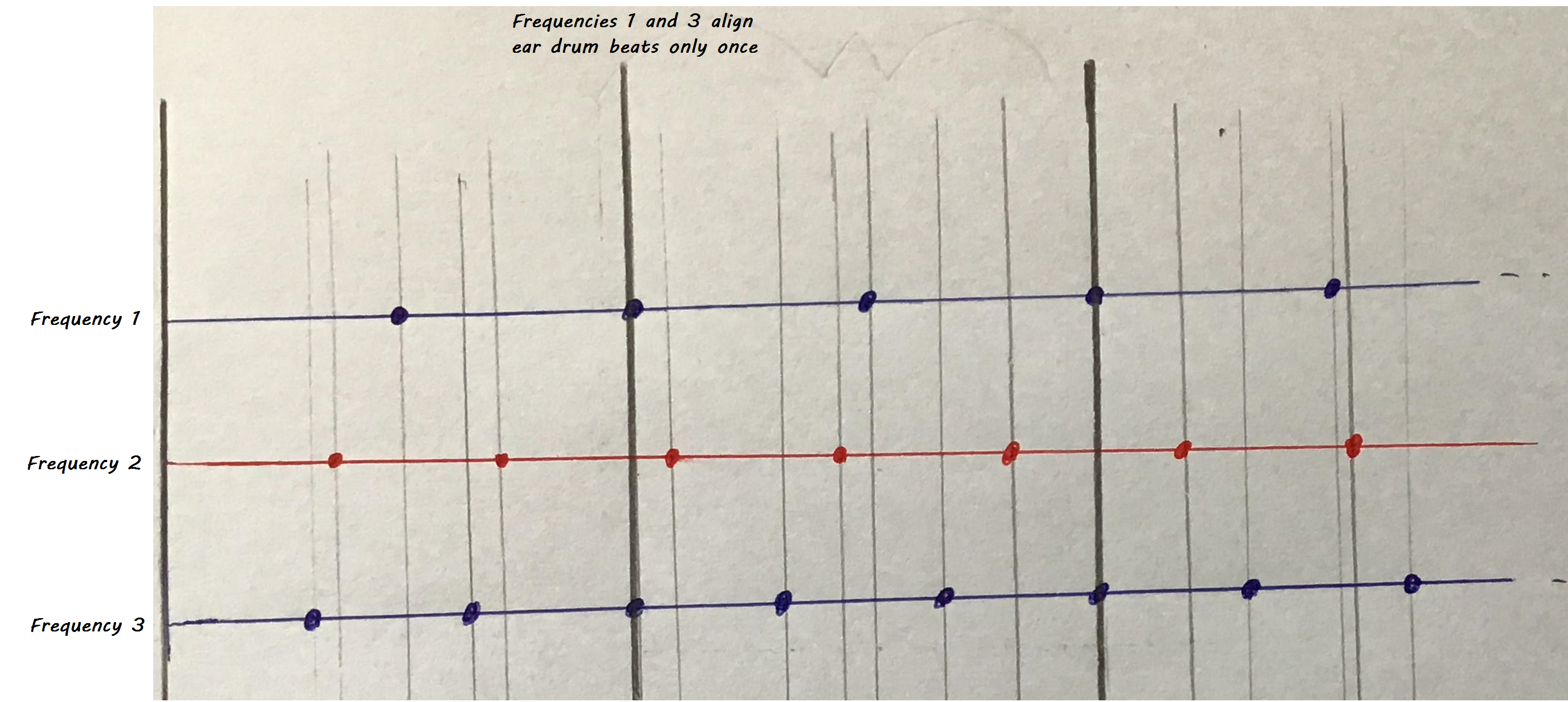 

Although today we know that Galileo was wrong – the eardrum works differently and is not solely responsible for hearing – it is still interesting to use this theory of consonance to gain insight as to why certain chords sound more consonant than others.

I have come up with a set of all 21 different triads. These for me are the 21 possible sonorities up to inversion. That is I consider  C E G the same as C F A – both major triads. In order to maintain some order I have voiced the 21 triads in closed position in one octave all with the lowest voice (not necessarily the ‘root’ note) being middle C. I have also enforced that they are to span the largest note range,  so when I needed to choose between say C E G and C F A I chose C F A because C to A is wider than C to G.